(DOSSIER) Texte précédent : INTRODUCTION
Texte suivant : LES MATHÉMATIQUES COMME SUJET DE CRÉATION
DES OUTILS MATHÉMATIQUES TRÈS UTILES
La géométrie est aux arts plastiques ce que la grammaire est à l’art de l’écrivain.
Guillaume Apollinaire
La relation entre les mathématiques et les arts s’inscrit dans l’histoire. Les artistes ont pu profiter au fil du temps de différents outils mathématiques. On ne saurait passer sous silence l’invention de la perspective qui a permis de donner l’illusion de la profondeur dans les tableaux ou la découverte des nouvelles géométries qui a inspiré l’éclatement des formes au XXe siècle.
Voici quelques exemples d’outils mathématiques exploités par les créateurs d’hier et d’aujourd’hui.
- La perspective
- Les lignes de composition
- Les proportions et le nombre d’or
- La symétrie et l’asymétrie
- Les transformations géométriques
- Les algorithmes et les formules mathématiques
- Les stratégies de classement
Ressources consultées
| Ressources | Éléments à approfondir |
 Site de Livres ouverts |
Observer les liens entre l’évolution des sciences (et des mathématiques) et l’histoire de l’art.
Exemples :
|
 Site de Livres ouverts |
S’informer sur l’évolution de la perspective en art :
|
 Site des Éditions Palette |
Découvrir l’univers du cubisme, un mouvement artistique qui bouleverse les conventions de la perspective classique.
« Au début du XXe siècle, quelques jeunes artistes, menés par Pablo Picasso et Georges Braque, révolutionnent le monde de l’art. Ils osent bouleverser les règles intangibles de la perspective et inventent ainsi le cubisme. Ces pionniers cherchent à représenter autrement la réalité, à tout montrer, même ce que l’on ne devrait pas voir — comme les deux yeux d’une femme de profil — et réduisent la nature à des formes géométriques. Un peu comme un cube que l’on aurait mis à plat! » (Extrait de Le cubisme, la réinvention de l’art) Avec les objets fragmentés du cubisme, on assiste à un véritable éclatement des formes! |
 Site des Éditions Taschen |
Plonger dans l’œuvre graphique de Maurits Cornelis Escher.
« En exposant mes sens aux énigmes de l’univers, en réfléchissant à ces sensations et en les analysant, je m’approche du domaine des mathématiques. » (Extrait de L’œuvre graphique) Observer différentes créations de l’artiste :
Découvrir l’importance des mathématiques dans les compositions de l’artiste. « Celui qui veut composer une symétrie sur une surface plane doit tenir compte des trois principes de la cristallographie : déplacements répétés (translation), pivotement autour d’un axe (rotation), reflet de l’image dans un miroir (réflexion). » (Extrait de L’œuvre graphique) |
 Site des Éditions Gallimard |
Découvrir certaines clés pour comprendre et apprécier un tableau.
Exemples de clés à saveur mathématique :
« Cézanne déclarait : “Il faut voir dans la nature des cylindres, des sphères et des cônes.” Ses compositions s’appuient souvent sur une forte structure géométrique. » (Extrait de Les clés de la peinture) |
|
Le regard du peintre : La composition picturale |
Découvrir différents secrets de la composition picturale.
Leon-Battista Alberti « fut le premier à employer le terme “composition” pour expliquer qu’un tableau était soumis à des lois mathématiques et géométriques claires et harmonieuses à l’exemple de la création du monde par Dieu. » (Extrait de Le regard du peintre : La composition picturale) Explorer divers schémas de composition :
|
| Ressources complémentaires |
| Parcelles d’infini : Promenade au jardin d’Escher Alain Nicolas Éditions Belin, 2006 Méthode de pavage figuratif Cézanne : Le père de l’art moderne Initiation à la composition et à la perspective Le grand livre de la composition |
EXEMPLES DE PISTES D’EXPLORATION
| EN GÉNÉRAL | |
| Pistes d’exploration | Exploitation du numérique |
| Rechercher des informations sur un outil mathématique en particulier et utiliser un moyen original de diffuser les découvertes. | Organiser les informations avec un idéateur :
Collectionner des illustrations :
Diffuser les informations :
* Accompagner les publications du mot-clic #artsetmaths. |
| LA PERSPECTIVE… BOULEVERSÉE! | |
| Pistes d’exploration | Exploitation du numérique |
| Transformer une photographie réaliste en une photographie cubiste. | Explorer le cubisme de manière ludique (observer quelques œuvres et transformer une photographie) :
Créer une image cubiste à partir de quelques photographies :
Exemples
|
| LES LIGNES DE COMPOSITION | |
| Pistes d’exploration | Exploitation du numérique |
| Observer les lignes de composition dans différentes œuvres et les effets produits. | Tracer les lignes de composition sur une œuvre et commenter :
Exemples
|
| Prendre des photographies en explorant la règle des tiers. | Utiliser l’appareil-photo et recadrer l’image au besoin.
Exemple
|
| LA SYMÉTRIE | |
| Pistes d’exploration | Exploitation du numérique |
| Vivre une chasse à la symétrie dans son environnement pour s’inspirer (nature, architecture, objets divers). | Photographier les découvertes :
Mettre en commun les découvertes :
|
| Créer des images photographiques en utilisant la symétrie. | Générer une symétrie :
Exemple
Utiliser une application de type kaléidoscope :
Exemple
|
| Explorer la répétition de motifs au moyen de la symétrie. | Utiliser une application de type kaléidoscope :
Astuces
Exemples
|
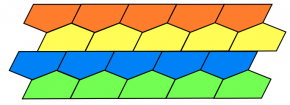
| LES TRANSFORMATIONS GÉOMÉTRIQUES | |
| Pistes d’exploration | Exploitation du numérique |
| Créer des dallages avec des motifs géométriques. Réflexion mathématique Explorer les figures géométriques qui permettent de paver le plan.
|
Utiliser une application de formes géométriques :
Exemples
Exemples
Exemple
Procédure possible : |
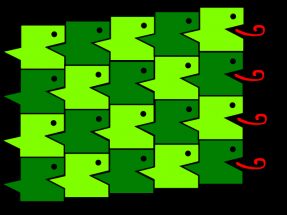
| Créer des dallages avec des motifs figuratifs à la manière d’Escher.
Pour s’inspirer… Méthode de pavage figuratif |
Utiliser une application de dessin vectoriel :
Utiliser une application de programmation :
|
| LES ALGORITHMES | |
| Pistes d’exploration | Exploitation du numérique |
| Créer une œuvre numérique en exploitant un logiciel de programmation. | Utiliser une application pour programmer :
Exemples
|
Art du rangement
Intention créative
Créer une œuvre photographique en deux parties (diptyque) en s’inspirant d’Ursus Wehrli.
| Ursus Wehrli (1969 — ) |
Informations tirées de… |
| Cet artiste pratique avec humour l’art du rangement. Cet art consiste à extraire les éléments d’une image, à les classer et à les agencer autrement pour créer une œuvre revisitée et inédite. « La vie est un bazar. Par chance, Ursus Wehrli la remet en ordre. » (Extrait de Photos en bazar) Site officiel de l’artiste Livres Exemples d’œuvres Dans son livre intitulé L’art en bazar, il s’amuse à ranger les tableaux de peintres célèbres comme Paul Klee, Vassily Kandinsky et René Magritte. Vidéo : Conférence TED d’Ursus Wehrli Dans l’ouvrage Photos en bazar, il met de l’ordre dans une variété de scènes du quotidien : une corde à linge, un carré de sable, un stationnement, un bol de fruits… Vidéo : « À l’envers du décor… » Ursus Wehrli explore divers critères de classement :
|
 Site des Éditions Milan
|
Inspiration
| Actions | Exploitation du numérique |
| Utiliser le livre Photos en bazar comme déclencheur. | |
| Présenter l’intention créative : créer une œuvre photographique en deux parties (diptyque) en s’inspirant d’Ursus Wehrli. | |
| S’inspirer des œuvres du livre ou de celles trouvées sur Internet. | Projeter les œuvres sur le TNI. |
Dégager les caractéristiques des œuvres.
|
Créer une mémoire collective numérique pour conserver et enrichir les idées.
Cette mémoire collective peut prendre différentes formes :
|
| Réflexion artistique Profiter de cette amorce pour vivre une démarche d’appréciation. |
Réalisation
| Actions | Exploitation du numérique |
| Réfléchir à différents contextes du quotidien dans lesquels on pourrait mettre de l’ordre : bac d’objets perdus, coffre à crayons, bac de jouets, bol de céréales, tiroir de bas… | Créer un organisateur graphique pour conserver les idées. |
| Choisir son contexte préféré et rassembler les objets nécessaires à la réalisation de l’œuvre. | |
Créer la première partie de l’œuvre :
Astuce |
Utiliser l’appareil-photo et recadrer au besoin. |
Créer la deuxième partie de l’œuvre :
Astuce
|
Utiliser l’appareil-photo et recadrer au besoin. |
| Choisir un titre humoristique. | |
| Placer les deux parties de l’œuvre sur un même support pour montrer le contraste entre les deux compositions. | Placer les deux parties de l’œuvre l’une en dessous de l’autre ou côte à côte et ajouter le titre :
Astuce
Exemples
Sofia, 11 ans |
Exemples de créations
Retour
| Actions | Exploitation du numérique |
| Observer et comparer les œuvres de ses pairs. | Projeter les œuvres sur le TNI. |
| Discuter des caractéristiques des œuvres et des effets produits sur l’observateur. Réflexion artistique Profiter de cette discussion pour vivre une démarche d’appréciation. |
|
| Dégager les critères de classement utilisés pour créer la deuxième partie des œuvres. | Enrichir la mémoire collective amorcée lors de l’observation des œuvres de l’artiste. |
| Compléter l’exploration des œuvres de l’artiste avec le livre l’Art en bazar. |
Diffusion
| Actions | Exploitation du numérique |
| Rassembler toutes les œuvres des élèves. | Créer un livre :
Créer un diaporama :
|
| Partager les œuvres sur les médias sociaux. | Publier sur le réseau de votre choix :
*Accompagner les publications du mot-clic #artsetmaths. |
—
Ceci est une partie d’un dossier complet.
SOMMAIRE DU DOSSIER
- Les liens qui unissent les mathématiques et les arts plastiques
- Vue d’ensemble
- Proposition
LES MATHÉMATIQUES COMME OUTIL POUR SOUTENIR LA CRÉATION
- Des outils mathématiques très utiles
- La perspective
- Les lignes de composition
- Les proportions et le nombre d’or
- La symétrie et l’asymétrie
- Les transformations géométriques
- Les algorithmes et les formules mathématiques
- Les stratégies de classement
- Exemples de pistes d’exploration
- Art du rangement
LES MATHÉMATIQUES COMME SUJET DE CRÉATION
- L’art abstrait à saveur géométrique
- Abstraction : Hommage à Kandinsky
- Abstraction : Le cercle sous toutes ses formes
- Art optique (Optical art) : Hommage à Vasarely
- L’art figuratif à saveur mathématique
- Photographie mathématique
- Le chiffrier
- Le récit à saveur mathématique
- Les illustrations exploitant les formes géométriques
- La fin d’un voyage… Le début de la création
- Remerciements
- Note sur les droits d’auteur
Recevez l'infolettre Hebdo mardi #Actu et vendredi #DevProf pour ne rien manquer des nouveautés de l'École branchée!
