Par Jocelyn Dagenais, enseignant de mathématiques de formation au secondaire, personne-ressource du RÉCIT au Centre de services scolaire des Hautes-Rivières
Texte présenté dans le cadre de la conférence de consensus sur l’utilisation du numérique en éducation organisée par le CTREQ, dont nous avons présenté un aperçu.
L’enseignement des mathématiques à l’école primaire, secondaire et fortement au collégial, s’adapte difficilement en matière d’intégration aux ressources et outils numériques que nous avons vus apparaître depuis plus de trente ans (Assude, 2007).
Le numérique transforme les façons de faire des mathématiques. Or, nous enseignons encore les mêmes méthodes de calculs, demandons de tracer des graphiques à main levée et travaillons la géométrie de la même façon que lorsque ces outils n’existaient pas!
Un peu d’histoire
Il y a 50 ans cette année, la compagnie Texas Instruments lançait sa première calculatrice, la Datamath. Dans les années 1970, les premières calculatrices de Texas Instruments (SR-50 en 1974) et Hewlett Packard (HP-35 en 1972) permettant d’effectuer des rapports trigonométriques faisaient leur apparition

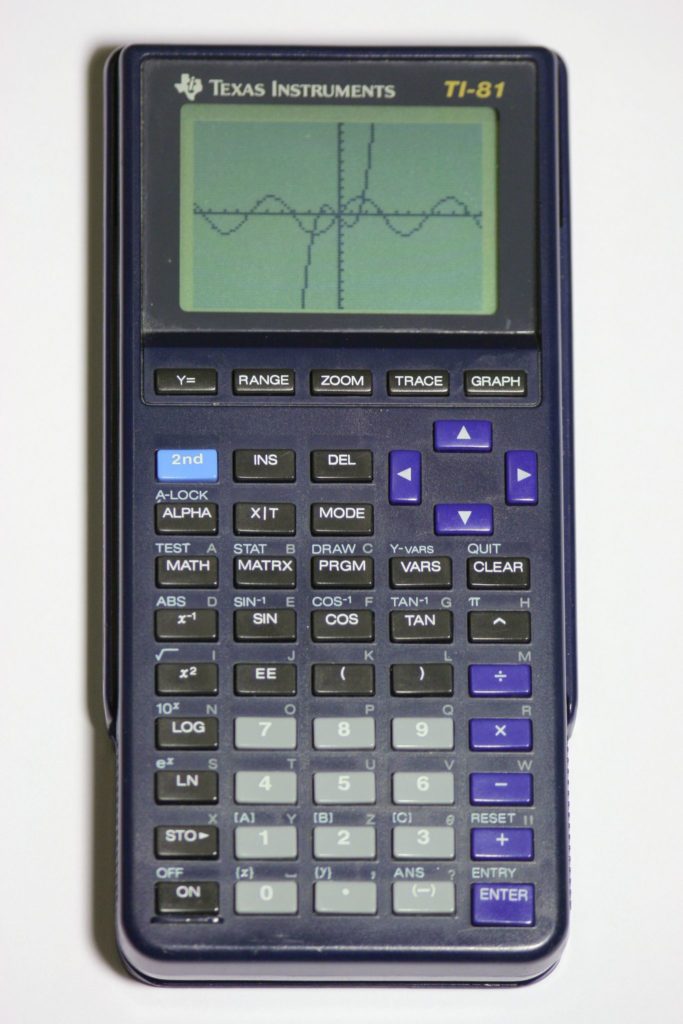
Les premières calculatrices à affichage graphique apparaissent en 1985 avec la Casio fx-7000G mais les plus populaires restent celles de Texas Instruments apparues en 1990 avec la TI-81. Avec elles, la possibilité de coordonner et de convertir rapidement différentes représentations sémiotiques (listes de nombres, table, règle, graphique) est accrue. À titre d’exemple, l’étude de l’influence de la valeur des paramètres des fonctions est facilitée, puisque l’outil offre rapidement une rétroaction à l’élève par le biais du graphique produit.
Le premier logiciel de géométrie dynamique qui sera utilisé dans les écoles du Québec est Cabri-géomètre (1986) et plusieurs autres logiciels ont fait leur apparition par la suite. Avec eux, l’exploration de propriétés ou de relations géométriques est favorisée et l’activité de preuve est modifiée (Laborde & Capponi, 1994).
Le travail de généralisation est aussi renforcé puisque l’outil permet d’étudier de multiples cas par simple déplacement de points libres. Dans ces micromondes, l’élève apprend à construire des objets en s’interrogeant sur leurs propriétés et leur conservation (Arzarello, Olivero, Paola & Robutti, 2002).
Dans les dernières années, nous avons vu des suites d’outils comme Geogebra (2001-2002) et Desmos (2011) permettant à l’enseignant de créer lui-même, de partager et de modifier des activités qui intègrent la géométrie dynamique, le tableur et la représentation graphique.
De même, des outils comme Photomath (2014) et Symbolab (2011) permettent aux élèves de voir les démarches complètes des techniques de calculs mathématiques. Pour terminer, la programmation par blocs a connu une ascension fulgurante dans les dernières années avec en particulier l’outil Scratch du MIT qui est sorti en 2007.
La programmation permet une approche par résolution de problèmes où l’élève est amené à produire des solutions créatives. Combinée avec la robotique, c’est une combinaison gagnante.
L’utilisation de la technologie en classe de mathématique
L’intégration de la technologie dans les cours de mathématique se fait toutefois à géométrie variable depuis plusieurs années et ce n’est pas étranger aux méthodes d’enseignement qui n’ont pas beaucoup évolué elles non plus.
Le modèle traditionnel du cours de mathématique où l’enseignant explique la théorie aux élèves qui doivent l’appliquer à travers différents exercices est encore bien présent. La plupart du temps, la technologie (s’il y en a) est utilisée par l’enseignant de mathématiques en avant de la classe, probablement sur un tableau numérique mais l’élève reste passif dans l’utilisation de la technologie.
Le débat n’est pas sur l’utilité de ces outils technologiques performants, mais bien sur la façon de les utiliser en salle de classe et de les intégrer à notre pédagogie.
Qui accepterait encore d’extraire une racine carrée à la main? De faire un graphique précis avec du papier quadrillé? Ou d’explorer les propriétés d’une transformation géométrique après avoir pris quinze minutes pour l’effectuer avec compas, équerre et règle?
L’idée maîtresse n’est pas d’évacuer tous ces outils et techniques, mais bien de les appréhender en tant que technologies situées à une époque donnée. Elles étaient, à ce moment, les meilleurs outils disponibles. Démontrer leurs usages demeure certes pertinent, mais une réflexion plus large s’avère nécessaire en termes d’intégration du numérique qui permet d’approcher de nouveaux problèmes dès le primaire et le secondaire et d’apprendre à les résoudre avec des outils dont l’apprentissage s’avérerait nécessaire pour assurer une plus solide formation scientifique.
L’enseignant doit trouver la valeur ajoutée de la technologie dans son enseignement:
- À quel moment dois-je utiliser la technologie? Laquelle?
- À quels moment les élèves vont-ils utiliser la technologie? Laquelle?
- Qu’est-ce que la technologie permet aux élèves de faire que le papier-crayon ne peut pas?
- Est-ce qu’introduire ou approfondir des concepts mathématiques à l’aide de situations intégrant la technologie est meilleur qu’un enseignement magistral de ces concepts?
- Est-ce que la technologie peut permettre à mes élèves de découvrir des concepts mathématiques? D’établir des conjectures? De résoudre des problèmes?
- Pourquoi j’utiliserais cet outil technologique plutôt qu’un autre?
- Quelles activités mathématiques sont possibles ou perçues différemment grâce à l’utilisation des TIC?
- Etc.
On peut aller plus loin et se demander si nos programmes de mathématiques actuels sont adaptés à l’utilisation de la technologie. La réponse est évidente: non. Prenons un contenu mathématique de quatrième secondaire, la corrélation linéaire et la droite de régression.
Il est bien indiqué dans la progression des apprentissages qu’au besoin, la détermination de la valeur du coefficient de corrélation pour les modèles à l’étude se fait à l’aide d’outils technologiques. Cependant, sur le terrain, on sait très bien que cet apprentissage n’est pas fait avec la technologie. Pourquoi ? Examen ministériel oblige, car ce contenu n’est jamais vérifié avec une question nécessitant de la technologie.
L’épreuve ministérielle influence l’utilisation de la technologie
L’épreuve ministérielle de mathématique de quatrième secondaire est sous la modalité du papier-crayon depuis son implantation. L’utilisation de la technologie lors de la passation de l’épreuve a évolué au fil du temps.
On dirait cependant qu’un élément n’a pas changé: on ne s’interroge pas si la formulation des questions demeure adaptée et pertinente aux technologies présentes et accessibles aux élèves.
Une analyse rapide des épreuves et des différents documents d’informations qui précèdent les moments de passation donne plutôt l’impression que l’on vérifie après l’élaboration de l’épreuve si la technologie permettrait de répondre plus facilement à certaines questions. Et dans l’affirmative, on précise des options qu’il n’est pas possible d’utiliser.
Si nous continuons de procéder de cette façon, il sera impossible de faire évoluer tant les activités d’apprentissage menées en classe que les activités d’évaluation qui devraient bien préparer la personne citoyenne de demain qui souhaite faire des mathématiques ou qui a besoin de ces mathématiques dans des métiers de différents domaines.
Avec une approche axée sur les résultats, les enseignants ressentent une pression de présenter et faire travailler les élèves avec des questions de type ministérielle. Et de ce fait, comme ce sont des questions plus traditionnelles (questions à choix multiples et à réponses courtes pour évaluer la maîtrise des concepts et des processus mathématiques, et des situations d’application), l’utilisation de la technologie est toujours mise de côté en premier du processus d’apprentissage.
À quoi cela servira-t-il à l’enseignant et aux élèves d’utiliser la technologie si elle n’est pas disponible lors de l’épreuve ministérielle?
Et cela n’influence pas seulement les enseignants de quatrième secondaire, mais une grande majorité des enseignants des niveaux inférieurs et supérieurs. En donnant l’impression que le recours à la technologie ne transforme pas les activités d’enseignement, d’apprentissage et d’évaluation, on ferme ainsi les yeux sur les iniquités qui sont présentes dans les différentes classes du Québec.
Pour les élèves qui apprennent dans des classes qui intègrent la technologie par le biais de la résolution de problèmes, le retour à des épreuves faisant fi des techniques apprises avec la technologie c’est comme si nous leur demandions d’utiliser une scie circulaire toute l’année et qu’on leur donnait droit à une égoïne pour l’épreuve ministérielle. Ce débat technologique existe aussi en première secondaire où l’on peut voir plusieurs modèles d’utilisation de la calculatrice scientifique: elle est permise, elle n’est pas permise, elle est permise à partir du mois de mai, etc.
L’impact des choix faits dans les épreuves ministérielles a un impact sur l’évaluation en générale.
En 2015, le Groupe des Responsables en Mathématique au Secondaire (GRMS) avait sondé plus de 500 enseignants, enseignantes, conseillères et conseillers pédagogiques sur l’évaluation à l ‘aide des TIC. Voici quelques constats suite à ce sondage:
1) il y a un désir (voire même une inquiétude) de s’assurer d’une équité quant à l’utilisation des TIC dans l’évaluation;
2) les participants reconnaissent que les seules technologies utilisées en évaluation (et pas dans tous les cas) sont les calculatrices;
3) il semble que le «niveau technologique» diffère grandement d’un enseignant à l’autre, tout comme leur ouverture à utiliser les TIC;
4) les participants affirment que les structures en place actuellement ne permettent pas d’utiliser les TIC dans l’évaluation en mathématiques de façon équitable pour tous.
Le GRMS était d’avis que les élèves qui avaient accès aux calculatrices à affichage graphique depuis 2001 lors de ces épreuves étaient avantagés par rapport à ceux qui ne l’avaient pas.
Dans le document disponible ici, plusieurs exemples sont fournis à partir de questions des épreuves.
La nécessaire réflexion sur la place des technologies en évaluation des mathématiques
À quand une vraie réflexion sur la place des technologies en évaluation des mathématiques dans le contexte d’une épreuve ministérielle?
Deux pistes intéressantes dans le rapport du Conseil supérieur de l’éducation de 2018, Évaluer pour que ça compte vraiment, étaient les suivantes:
« Les épreuves officielles permettraient de “prendre une photo” de l’État du Québec à un moment donné. Cette “photo” devrait être destinées aux enseignants, pour un ajustement des pratiques, et soutenir la professionnalisation de l’acte d’évaluer. Toutefois, les résultats des épreuves sont connus pendant les vacances et aucun moment n’est consacré à une réflexion collective, ce qui permettrait de décider ce que l’on veut développer chez les élèves (notamment pour pouvoir communiquer des attentes claires). »
« Si les épreuves obligatoires n’étaient pas comptabilisés dans les résultats des élèves, elles pourraient jouer un rôle dans le pilotage du système sans entraîner les dérives soulignées. »
En voyant l’épreuve comme un levier pour améliorer les pratiques évaluatives, l’intégration des technologies ne serait plus vue du tout de la même façon.
Ce présent texte force au constat que la réflexion sur l’intégration du numérique en classe ne peut être laissée à la discrétion de chaque enseignante et enseignant, ni même à celle d’une équipe-école, d’une équipe d’un centre de services scolaire.
Le Ministre par la voie de son ministère de l’Éducation doit engager ses équipes responsables des apprentissages, de l’évaluation et de la sanction dans un mandat clair du virage numérique que l’on souhaite que le Québec prenne. Une réflexion systémique menée par chaque individu intéressé ou intervenant de près ou de loin dans l’enseignement des mathématiques semble plus que nécessaire.
Les questions qui suivent pourraient alors alimenter cette réflexion :
- Est-ce que notre enseignement des mathématiques actuel est adapté dans le monde technologique dans lequel on vit?
- Quel est la place du calcul (mental et écrit) dans un contexte technologique?
- Est-ce normal qu’un élève termine son cours secondaire sans jamais avoir utilisé certains outils technologiques comme un tableur par exemple?
- Comment la technologie permet d’être créatif en mathématiques?
- Est-ce que les activités technologiques permettent aux élèves d’avoir des conversations mathématiques entre eux et avec l’enseignant?
- Est-ce que les activités technologiques proposées sont uniquement avec une rétroaction immédiate, c’est-à-dire bonne ou mauvaise réponse?
- Comment la rétroaction est-elle donnée lors de vos activités technologiques en mathématiques? Est-ce qu’elle donne du sens au raisonnement des élèves?
- Est-ce que les activités technologiques proposées créent un besoin intellectuel pour des nouvelles compétences mathématiques?
- Est-ce que les activités technologiques en mathématiques permettent de faire des estimations avant les calculs? Des conjectures avant les preuves? Des esquisses avant les graphiques? Des explications en mots avant les règles algébriques? Du langage de tous les jours avant le langage mathématique?
- Est-ce que les activités technologiques proposées permettent aux élèves d’avoir raison et/ou tort de différentes façons?
- Est-ce que les activités mathématiques proposées permettent aux élèves d’utiliser une variété d’outils technologiques?
- Quels sont les concepts mathématiques qui peuvent être approfondis avec la technologie? (Pistes: Mathématiques financières, statistiques, probabilités, etc.)
- Comment pourrait être utilisée la technologie dans un contexte d’évaluation mathématique?
RÉFÉRENCES BIBLIOGRAPHIQUES
Arzarello, F., Olivero, F., Paola, D. et al. A cognitive analysis of dragging practises in Cabri environments. Zentralblatt für Didaktik der Mathematik 34, 66–72 (2002).
Assude, T. (2007). Changements et résistances à propos de l’intégration des nouvelles technologies dans l’enseignement mathématique au primaire, Researchgate.
Conseil supérieur de l’éducation (2019). Évaluer pour que ça compte vraiment. Rapport sur l’état et les besoins de l’éducation 2016-2018. Québec.
Laborde, C. & Capponi, B. (1994). Cabri-géomètre constituant d’un milieu pour l’apprentissage de la notion de figure géométrique, Recherches en didactiques des mathématiques, 14 (1-2), 165- 210.